Part 3: A Humble Revisit

Writing data structures in Rust is a humbling experience.

Prior to this project, my most extensive data structure design was a very simple FIFO stack in Rotoscope. I've also never written more than toy projects in Rust. For some reason, I was convinced I could figure things out as I went here, randomly slapping lifetimes onto structs and functions, and flipping between accessing raw pointers and mutable references. I tried this approach for...way too long.

And so, the other day I finally cracked open the Rustonomicon and read it front to back, rather than skimming only the parts I thought I needed. There’s a ton of value in this resource if you need to do anything non-standard (i.e. raw pointers, memory allocation).

After reading that guide, I spent a couple of hours and had a safe, working version of my structure! Or rather, the frame of my structure. There are lots of rough edges and incorrect assumptions still in this code.

Heck, I’m probably still misusing lifetimes.

Struct & Enum Changes

StaticSearchTree<'a, K, V>

This is what my main structure looks like now:

- struct StaticSearchTree<K: Eq, V> {
-   memory: Pin<Box<[Node<K, V>]>>,
-   root: NonNull<Node<K, V>>,
-   _pin: PhantomPinned,
+ pub struct StaticSearchTree<'a, K: Eq + Ord + 'a, V: 'a> {
+   nodes: Box<[Node<'a, K, V>]>,
+   cells: Box<[Cell<'a, K, V>]>,
  }

The key concept I glossed over before was that the data I allocated up front actually needed to be owned by some object so that it could be carried through the program. Otherwise, it’s a memory leak or might get freed while a raw pointer was still referencing it (I spent way too long debugging this exact problem). I tried to pretend like I was writing C, allocating memory, having a raw pointer reference it, and hoping for the best. That doesn't work.

Node<'a, K, V>

- enum Node<K: Eq, V> {
-   Leaf(Element<K>, Block<K, V>),
+ enum Node<'a, K: Eq + Ord, V> {
+   Leaf(Key<K>, Block<'a, K, V>),
    Branch {
-     min_rhs: Element<K>,
-     left: MaybeUninit<NonNull<Node<K, V>>>,
-     right: MaybeUninit<NonNull<Node<K, V>>>,
+     min_rhs: Key<K>,
+     left: MaybeUninit<*const Node<'a, K, V>>,
+     right: MaybeUninit<*const Node<'a, K, V>>,
+     _marker: PhantomData<&'a Node<'a, K, V>>,
    },
  }

The Node enum has ditched the NonNull<T> construct one favour of a raw *const T pointer. I might switch this back, but It definitely helped simplify the moving parts in my head. Plus it’s safer to use correctly since there’s no access to a method like NonNull::as_mut to tempt me towards danger. We shouldn’t need to update these pointers until a resize event, at which point I’ll probably need to revisit this decision 🙃

Block<'a, K, V>

- struct Block<K: Eq, V> {
-   min_key: Element<K>,
-   max_key: Element<K>,
-   cells: NonNull<[Cell<K, V>]>,
+ struct Block<'a, K: Eq + Ord, V> {
+   min_key: Key<K>,
+   max_key: Key<K>,
+   cell_slice_ptr: *const Cell<'a, K, V>,
+   length: usize,
+   _marker: PhantomData<&'a [Cell<'a, K, V>]>,
  }

The block now has a *const T reference to the relevant slice of cells via cell_slice_ptr, and also some PhantomData to make it clear to the compiler that we’re holding a reference inside of this struct that’s tied to the lifetime of whatever instantiated this object. I also renamed Element<T> to Key<T> to help myself when reading the code to know that this is specific to key ordering.

Cell<'a, K, V>

- struct Cell<K, V> {
+ struct Cell<'a, K: 'a, V: 'a> {
    version: AtomicU16,
    marker: AtomicPtr<Marker<K, V>>,
    empty: UnsafeCell<bool>,
    key: UnsafeCell<Option<K>>,
    value: UnsafeCell<Option<V>>,
+   _marker: PhantomData<&'a Marker<K, V>>,
  }

Not much is different with Cell<K, V> except the added lifetime and added marker.

Initializing the Tree

Now that our data structures are (somewhat) sorted, we can dig in a little deeper on the actual initialization logic for the tree. I'll abbreviate some of the snippets to focus on they key pieces, but you can always view the current version on the GitHub repo.

This is the most simple test that we want to make pass:

#[cfg(test)]
mod tests {
  use crate::StaticSearchTree;

  #[test]
  fn test() {
    let mut tree = StaticSearchTree::<u8, &str>::new(30);
    tree.add(6, "World!");
    tree.add(5, "Hello");
    assert_eq!(tree.find(5), Some("Hello!"));
  }
}

The first bit of functionality we need to implement is instantiating the tree. For now, I'm treating the tree as in-memory only, but we'll probably want to persist this on disk at some point, and the allocation steps will need to move from memory blocks to files.

Don't worry (I tell myself), we'll keep things simple for now.

impl<'a, K: 'a, V: 'a> StaticSearchTree<'a, K, V>
where
  K: Eq + Copy + Ord + std::fmt::Debug + Copy,
  V: std::fmt::Debug + Copy,
{
  pub fn new(num_keys: u32) -> Self {
    /* We'll allocate the tree here */
  }
}

These are the steps for our instantiation:

1. Allocate a contiguous block to store all of the tree values:

// Box<[MaybeUninit<Cell<K, V>>]>
let mut cells = Self::allocate_leaf_cells(num_keys);

2. Allocate another contiguous block to store the tree nodes:

// Box<[MaybeUninit<Node<K, V>>]>
let mut nodes = Self::allocate_nodes(cells.len());

3. Recursively initialize all nodes in the tree:

// Vec<&mut Node<K, V>>
let mut leaves = Self::initialize_nodes(&mut *nodes, None);

4. Partition the block of values (from Step 1) into subsections and link to tree leaves:

let size = num_keys;
let slot_size = f32::log2(size as f32) as usize; // https://github.com/rust-lang/rust/issues/70887
let left_buffer_space = cells.len() >> 2;
let left_buffer_slots = left_buffer_space / slot_size;
let mut slots = cells.chunks_exact_mut(slot_size).skip(left_buffer_slots);

for leaf in leaves.iter_mut() {
  Self::finalize_leaf_node(leaf, slots.next().unwrap());
}

5. Return the StaticSearchTree holding all of the allocated data:

let initialized_nodes = unsafe { nodes.assume_init() };
let initialized_cells = unsafe { cells.assume_init() };

let active_cells_ptr_range = std::ops::Range {
  start: &initialized_cells[left_buffer_space] as *const _,
  end: &initialized_cells[initialized_cells.len() - left_buffer_space] as *const _,
};

StaticSearchTree {
  cells: initialized_cells,
  nodes: initialized_nodes,
  active_cells_ptr_range,
}

I've already covered the math for the first two allocations in Part 1, so I'll skip ahead to Step 3, which is really fun.

Recursively Initializing the Nodes

Let's start with the method signature:

pub fn new(num_keys: u32) -> Self {
  let mut cells = Self::allocate_leaf_cells(num_keys);
  let mut nodes = Self::allocate_nodes(cells.len());

  let mut leaves = Self::initialize_nodes(&mut *nodes, None);
  // ...
}

fn initialize_nodes<'b>(
  nodes: &'b mut [MaybeUninit<Node<'a, K, V>>],
  parent_node: Option<*mut *const Node<'a, K, V>>,
) -> Vec<&'b mut Node<'a, K, V>> {
  /* We'll initialize the nodes here */
}

StaticSearchTree::initialize_nodes takes a reference to some slice of uninitialized nodes, has an optional second argument (we'll get to that later), and returns a Vec<_> that holds mutable references to initialized nodes. Smells like initialization to me!

The reason we return a Vec<_> from this method rather than a slice is a few-fold: This method is actually recursive, returning variable-length collections depending on the phase, and the end-result of the recursion is a list of references to leaves in the tree. That collection is allocated and initialized within the method, and you can't return references to privately allocated data in Rust. Since slices are actually just &[_], they can only be referred to in reference-form, and so cannot be used here (as I understand it).

The more interesting thing here is the recursive design of the method, which produces the van Emde Boas layout we need for the cache-oblivious design. The logic goes like this:

1. Aim to reduce the node list to the smallest tree possible
2. Split the contiguous block of nodes at the middle of the tree, and recursively initialize the top half of the tree
3. Split the remaining nodes for the lower part of the tree by the number of leaves returned by the top half of the tree
4. Recursively initialize each of the branches of the lower half of the tree

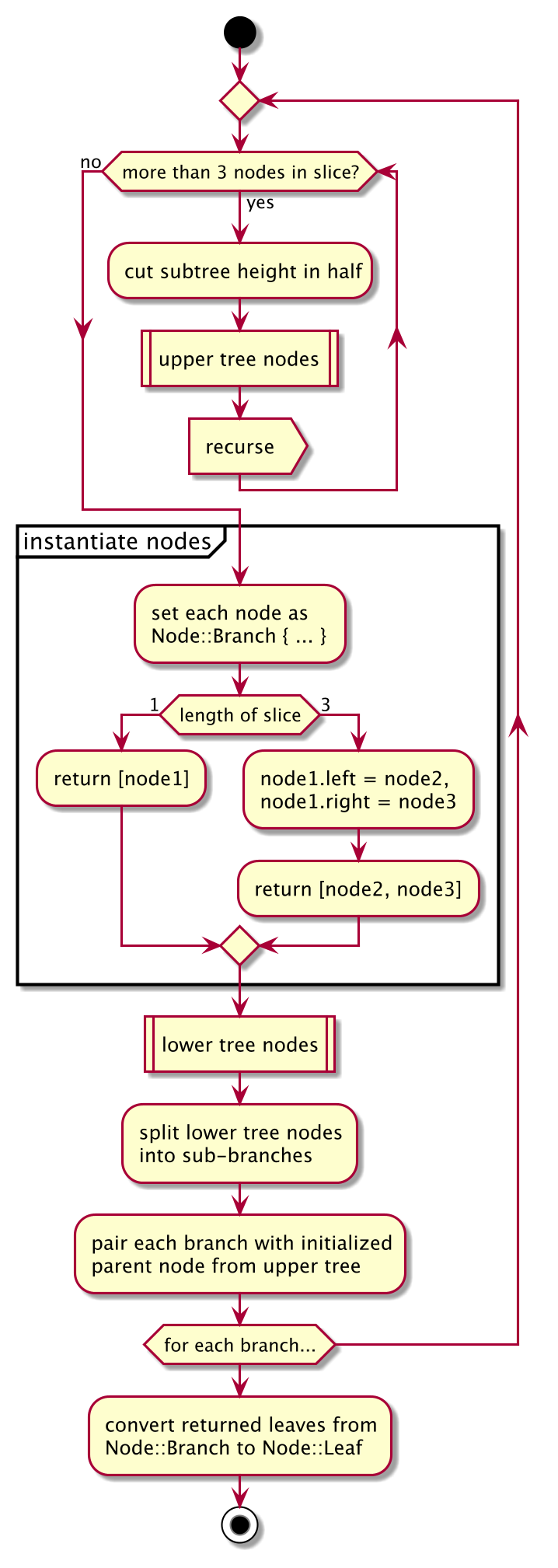
1. Aim to reduce the node list to the smallest tree possible

Depending on if the tree has an even or odd height, the smallest tree possible is either 1 or 3 nodes. Once we're given a list of <= 3 nodes, we initialize them. Recursion always needs an exit path, so this is ours.

if nodes.len() <= 3 {
  return Self::assign_node_values(nodes, parent_node);
}

2. Split the contiguous block of nodes at the middle of the tree, and recursively initialize the top half of the tree:

  let (upper_mem, lower_mem) = Self::split_tree_memory(nodes);
  let leaves_of_upper = Self::initialize_nodes(upper_mem, parent_node);

fn split_tree_memory<'b>(
  nodes: &'b mut [MaybeUninit<Node<'a, K, V>>],
) -> (
  &'b mut [MaybeUninit<Node<'a, K, V>>],
  &'b mut [MaybeUninit<Node<'a, K, V>>],
) {
  let height = f32::log2(nodes.len() as f32 + 1f32);
  let lower_height = ((height / 2f32).ceil() as u32).next_power_of_two();
  let upper_height = height as u32 - lower_height;

  let upper_subtree_length = 2 << (upper_height - 1);
  nodes.split_at_mut(upper_subtree_length - 1)
}

3. Split the remaining nodes for the lower part of the tree by the number of leaves returned by the top half of the tree:

let num_lower_branches = upper_mem.len() + 1;
let nodes_per_branch = lower_mem.len() / num_lower_branches;
let mut branches = lower_mem.chunks_exact_mut(nodes_per_branch);

4. Recursively initialize each of the branches of the lower half of the tree

Since StaticSearchTree::initialize_nodes always returns the leaves of whatever tree it completed initializing, we can rely on the return value from initializing the upper half of the tree to use as the list of nodes we need to stitch each branch from the lower half onto.

leaves_of_upper
  .into_iter()
  .flat_map(|subtree_leaf| match subtree_leaf {
    Node::Leaf(_, _) => unreachable!(),
    Node::Branch { left, right, .. } => {
      let lhs_mem = branches.next().unwrap();
      let rhs_mem = branches.next().unwrap();
      let lhs = Self::initialize_nodes(lhs_mem, Some(left.as_mut_ptr()));
      let rhs = Self::initialize_nodes(rhs_mem, Some(right.as_mut_ptr()));
      lhs.into_iter().chain(rhs.into_iter())
    }
  })
  .collect::<Vec<_>>()

Amazingly, at the end of all of this we end up with an internally-connected tree and we can return the final Vec<_> that contains just the final tree leaves!

5. Convert the returned nodes into Node::Leaf enums

During the recursion, we don't know whether we're in the middle of the tree or at the very ends. As a safe default, each node is initialized as a Node::Branch with the assumption that it will be paired with a left and right branch below it in the recursion.

Once we come back from the call to #initialize_nodes, the Vec<_> of nodes returned contains only the final leaves of the tree. We can iterate that list and convert each of them to Node::Leaf objects, passing each a subslice of the values memory block to store data:

fn finalize_leaf_node<'b>(
  leaf: &'b mut Node<'a, K, V>,
  leaf_mem: &'b mut [MaybeUninit<Cell<'a, K, V>>],
) -> () {
  match leaf {
    Node::Branch { min_rhs, .. } => {
      let length = leaf_mem.len();
      let initialized_mem = Self::init_cell_block(leaf_mem);
      let ptr = initialized_mem as *const [Cell<K, V>] as *const Cell<K, V>;
      let block = Block {
        cell_slice_ptr: ptr,
        length,
        _marker: PhantomData,
      };
      *leaf = Node::Leaf(*min_rhs, block);
    }
    Node::Leaf(_, _) => (),
  };
}

fn init_cell_block<'b>(
  cell_memory: &'b mut [MaybeUninit<Cell<'a, K, V>>],
) -> &'b mut [Cell<'a, K, V>] {
  for cell in cell_memory.iter_mut() {
    let marker = Box::new(Marker::<K, V>::Empty(1));
    cell.write(Cell {
      version: AtomicU16::new(1),
      marker: AtomicPtr::new(Box::into_raw(marker)),
      key: UnsafeCell::new(None),
      value: UnsafeCell::new(None),
      _marker: PhantomData,
    });
  }
  unsafe { MaybeUninit::slice_get_mut(cell_memory) }
}

Phew! Once all of those steps are done, we've got a tree laid out in van Emde Boas format pointing to a contiguous block of values that we can scan from left-to-right for range searches.

On the next post, I'll go over the steps to "add" a new value to our data structure!